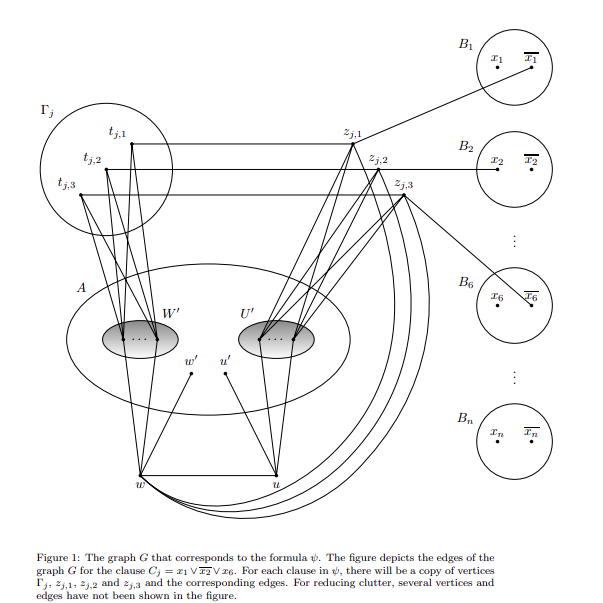
Reducing $(k,i)$-coloring to 3-SATAbstract
In an undirected graph, a proper $(k,i)$-coloring is an assignment of a set of colors to each vertex such that any two adjacent vertices have at most common colors. The $(k,i)$-coloring problem is to compute the minimum number of colors required for a proper $(k,i)$-coloring. This is a generalization of the classical graph coloring problem. We design a parameterized algorithm for the $(k,i)$-coloring problem with the size of the feedback vertex set as a parameter. Our algorithm does not use tree-width machinery, thus answering a question of Majumdar, Neogi, Raman and Tale [CALDAM 2017]. We also give a faster exact algorithm for $(k,k-1)$-coloring. From the hardness perspective, we show that the $(k,i)$-coloring problem is NP-complete for any fixed values $i$, $k$, whenever $i < k$, thereby settling a conjecture of Méndez-Díaz and Zabala (1999) and again asked by Majumdar, Neogi, Raman and Tale. The NP-completeness result improves the partial NP-completeness shown in the preliminary version of this paper published in CALDAM 2018.
Saurabh Joshi
Principal Researcher
My research interests include Blockchain, Distributed Systems, Constraint Programming, Formal Verification, Programming Languages and Program Analysis.